• 1. 机器学习的分类
  • 1.1. 有监督
    • 1.1.1. 分类问题（classification problen）
    • 1.1.2. 回归问题（regression problem）
      • 1.1.2.1. 线性回归
      • 1.1.2.2. 非线性回归
  • 1.2. 无监督
  • 1.3. 强化学习
• 2. 代价函数（cost function）
• 3. 梯度下降算法（gradient descent algorthm）
  • 附录

1. 机器学习的分类

1.1. 有监督

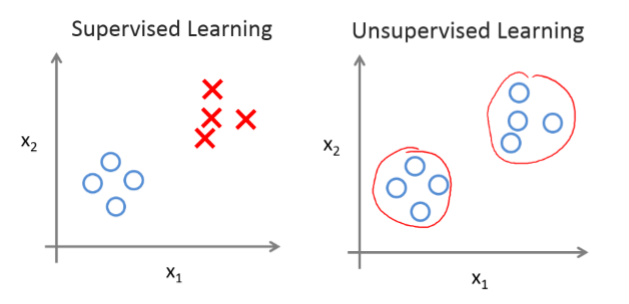
监督学习(supervised learning)：通过已有的训练样本（即已知数据以及其对应的输出）来训练，从而得到一个最优模型，再利用这个模型将所有新的数据样本映射为相应的输出结果，对输出结果进行简单的判断从而实现分类的目的，那么这个最优模型也就具有了对未知数据进行分类的能力。

监督学习中只要输入样本集,机器就可以从中推演出制定目标变量的可能结果.如协同过滤推荐算法,通过对训练集进行监督学习,并对测试集进行预测,从而达到预测的目的。监督学习方法又分为生成方法（generative approach）和判别方法（discriminative approach），所学到的模型分别称为生成模型和判别模型。
判别方法：由数据直接学习决策函数$Y=f(X)$或者条件概率分布$P(Y|X)$作为预测模型，即判别模型。基本思想是有限样本条件下建立判别函数，不考虑样本的产生模型，直接研究预测模型。典型的判别模型包括k近邻、感知机、决策树、支持向量机等。
生成方法：从数据学习联合概率密度分布$P(X,Y)$，然后求出条件概率分布$P(Y|X)$作为预测模型，即生成模型$P(Y|X)=P(X,Y)/P(X)$。基本思想是先建立样本的联合概率密度模型$P(X,Y)$，然后得到后验概率$P(Y|X)$，再利用它进行分类。这里是先求出$P(X,Y)$才得到$P(Y|X)$的，然后了这个过程还得先求出$P(X)$。$P(X)$就是你的训练模型的概率分布。这样的方法之所以称为生成方法，是因为模型表示了给定输入X产生输出Y的生成关系，用于随机生成观察值建模，特别是在给定某些隐藏参数的情况下。典型的生成模型有朴树贝叶斯模型、隐马尔科夫模型等。

1.1.1. 分类问题（classification problen）

1.1.2. 回归问题（regression problem）

1.1.2.1. 线性回归

1.1.2.2. 非线性回归

1.2. 无监督

无监督学习(unsupervised learning)：我们事先没有任何训练数据样本，需要直接对数据进行建模。比如我们去参观一个画展，我们对艺术一无所知，但是欣赏完很多幅作品之后，我们面对一幅新的作品之后，至少可以知道这幅作品是什么派别的吧，比如更抽象一些还是更写实一点，虽然不能很清楚的了解这幅画的含义，但是至少我们可以把它分为哪一类。再比如我们在电影院看电影，对于之前没有学过相关电影艺术知识的我们，可能不知道什么是一部好电影，什么是一部不好的电影，可是在观看了很多部电影之后，我们脑中对电影就有了一个潜在的认识，当我们再次坐在电影院认真观看新上映的电影时，脑中就会对这部电影产生一个评价：怎么这电影这么不好啊，整个故事线是混乱的，一点也不清晰，比我之前看过的那些电影差远了，人物的性格也没有表现出来，关键是电影主题还搞偏了；哎呀，这个电影拍得确实好啊，故事情节和人物性格都很鲜明，而且场景很逼真，主角的实力表演加上他与生俱来的忧郁眼神一下把人物演活了。非监督学习的常见算法包括A priori算法及K-Means算法。

1.3. 强化学习

强化学习其实就是一个连续决策的过程。强化学习不给数据做标注，而是给一个回报函数，这个回报函数决定当前的状态得到什么样的结果（“好”还是“坏”），其数学本质是一个马尔科夫决策过程。最终的目的是决策过程中整体地回报函数期望最优。

2. 代价函数（cost function）

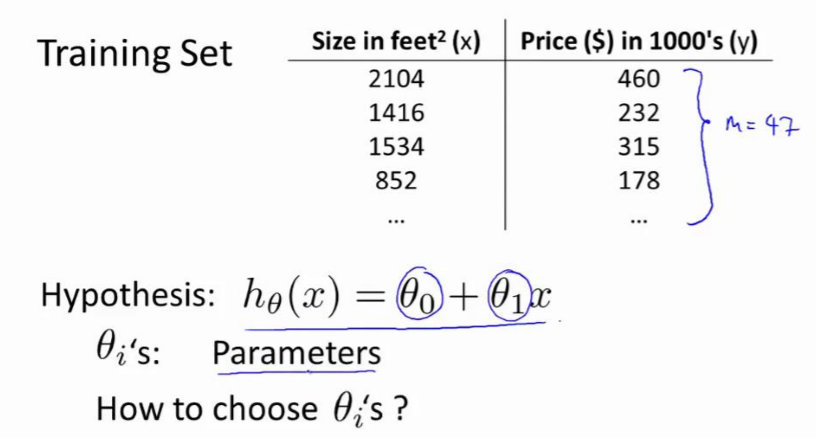
在线性回归中我们有一个像这样的训练集，m 代表了训练样本的数量，比如 m = 47。
而我们的假设函数，也就是用来进行预测的函数，是这样的线性函数形式：$h_{\theta}(x)=\theta_{0}+\theta_{1}x$

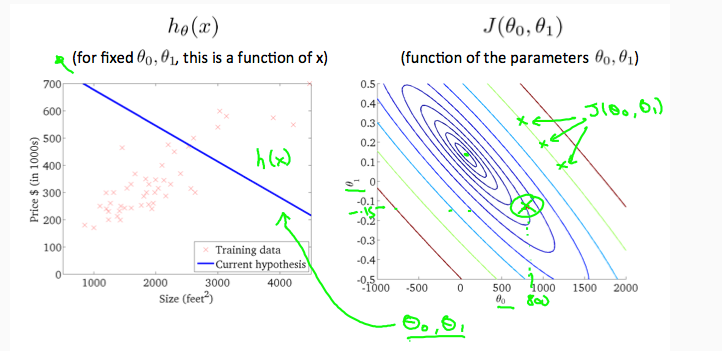
我们现在要做的便是为我们的模型选择合适的参数（parameters）$\theta_{0}$和$\theta_{1}$。我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

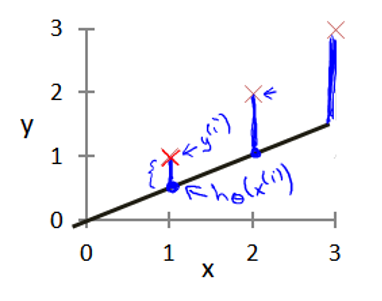
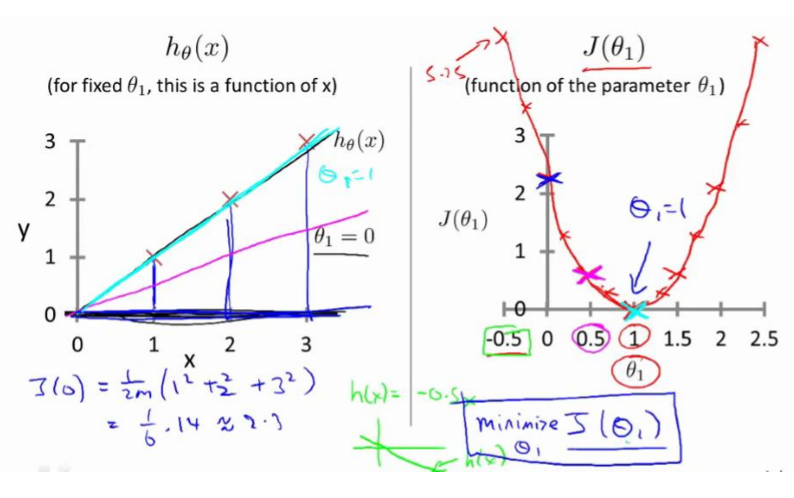
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得代价函数$J(\theta_{0},\theta_{1})=\frac 1 2m \sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2$最小。
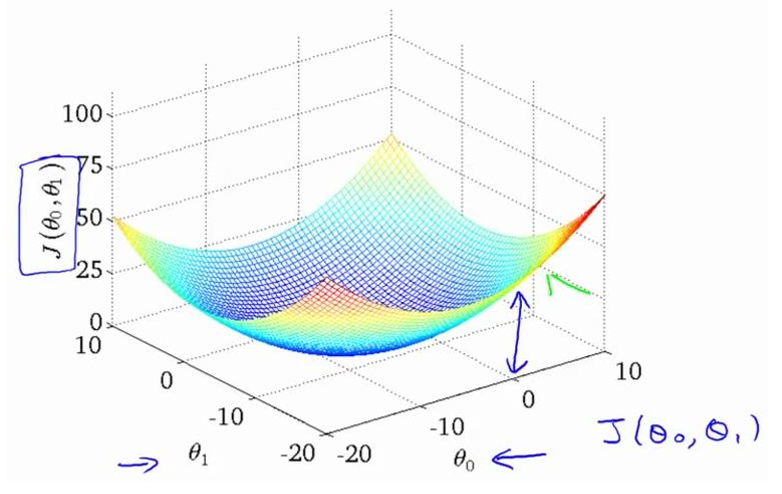
我们绘制一个等高线图，三个坐标分别为$\theta_{0}$，$\theta_{1}$和$J(\theta_{0},\theta_{1})$：
则可以看出在三维空间中存在一个使得$J(\theta_{0},\theta_{1})$最小的点。
代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

Hypothesis:
$h_{\theta}x= \theta_1$
Parameters:
$\theta_1$
Cost Function:
$J(\theta_1)=\frac 1 2m \sum_{i=1}^m (h_{\theta}x^{(i)}-y^{(i)})^2$
Goal:
$\mathop{minimize}\limits_{\theta_1} J(\theta_1)$

Hypothesis:
$h_{\theta}x=\theta_0 + \theta_1$
Parameters:
$\theta_0, \theta_1$
Cost Function:
$J(\theta_0, \theta_1)=\frac 1 2m \sum_{i=1}^m (h_{\theta}x^{(i)}-y^{(i)})^2$
Goal:
$\mathop{minimize}\limits_{\theta_0, \theta_1} J(\theta_0, \theta_1)$

3. 梯度下降算法（gradient descent algorthm）

批量梯度下降（batch gradient descent）算法的公式为：
repeat untill convergence{
$\theta_j := \theta_j - \alpha\frac {\partial} {\partial \theta_j} J(\theta_0, \theta_1) for( i = 0 and j = 1 )$ }
其中 α 是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。其中 α 不能太大也不能太小：太大可能会导致发散；太小可能会使训练时间变得很长。
在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新 θ0 和 θ1 。

$temp0 := \theta_0 - \alpha\frac {\partial} {\partial \theta_0} J(\theta_0, \theta_1)$
$temp1 := \theta_1 - \alpha\frac {\partial} {\partial \theta_1} J(\theta_0, \theta_1)$
$\theta_0 := temp0$
$\theta_1 := temp1$

在梯度下降算法中，这是正确实现同时更新的方法。我不打算解释为什么你需要同时更新，同时更新是梯度下降中的一种常用方法。我们之后会讲到，同步更新是更自然的实现方法。当人们谈到梯度下降时，他们的意思就是同步更新。

特征缩放（feature scaling）是用来标准化数据特征的范围。特征缩放还可以使机器学习算法工作的更好。比如在K近邻算法中，分类器主要是计算两点之间的欧几里得距离，如果一个特征比其它的特征有更大的范围值，那么距离将会被这个特征值所主导。因此每个特征应该被归一化，比如将取值范围处理为0到1之间。
特征缩放方法一：调节比例（rescaling）
这种方法是将数据的特征缩放到[0,1]或[-1,1]之间。缩放到什么范围取决于数据的性质。对于这种方法的公式如下：
$x^' = \frac {x-min(x)} {max(x)-min(x)}$
特征缩放方法二：标准化（standardization）
特征标准化使每个特征的值有零均值(zero-mean)和单位方差(unit-variance)。这个方法在机器学习地算法中被广泛地使用。例如：SVM，逻辑回归和神经网络。这个方法的公式如下：
$x^' = \frac {x-\bar{x}} {max(x)-min(x)}$

附录

• m 代表训练集中实例的数量
• x 代表特征/输入变量
• y 代表目标变量/输出变量
• (x,y) 代表训练集中的实例
• (x⁽ⁱ⁾,y⁽ⁱ⁾) 代表第 i 个观察实例